Understanding Bayes
What is Bayes’ Theorem?
Bayes’ Theorem is a fundamental concept in probability theory that describes how to update the probability of a hypothesis as new evidence becomes available.
Bayes formula is: $P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}$
It’s widely used in fields like medicine, machine learning, and many others where we need to make inferences based on incomplete or uncertain data.
 Bayes and Streamlit?
Bayes and Streamlit?Let’s break down Bayes’ Theorem and its components.
The Formula: The mathematical expression of Bayes’ Theorem is
P(A|B) = [P(B|A) * P(A)] / P(B)Which leads to this interesting 3d behaviour (having P(A) constant )
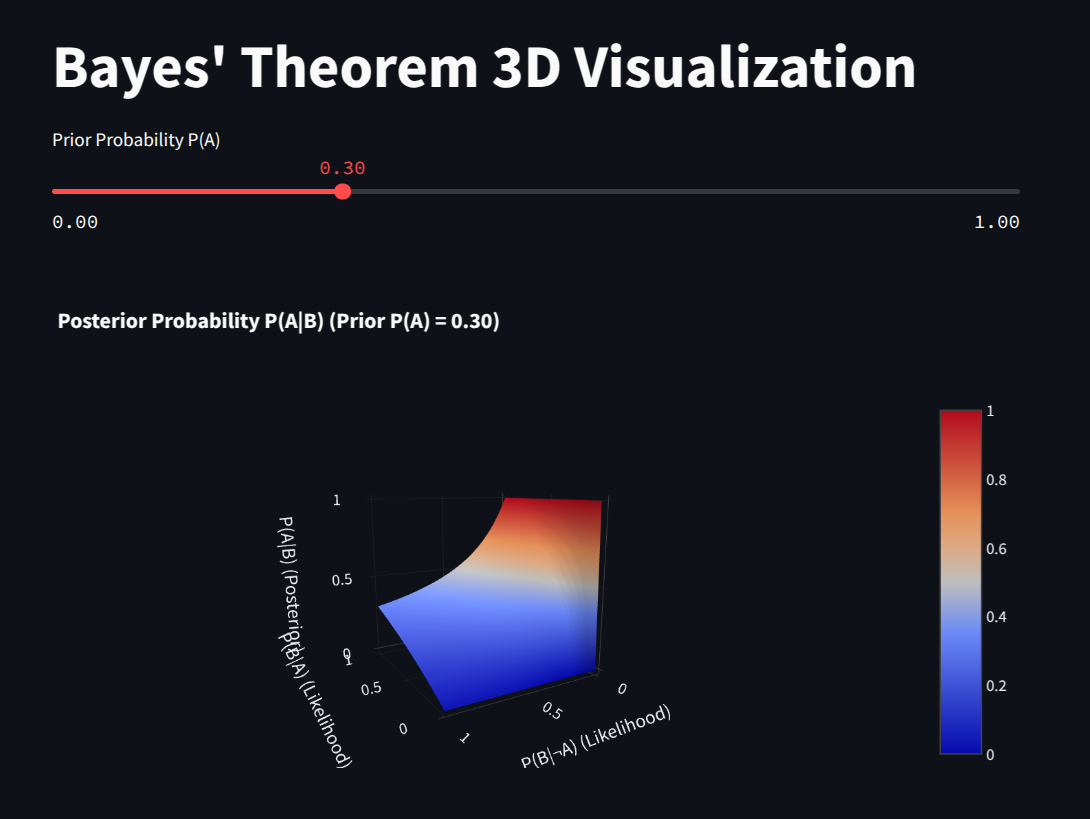
Understanding the Terms:
P(A|B) (Posterior Probability): This is the probability of hypothesis A being true given that we have observed evidence B. It’s what we want to calculate – our updated belief about A after considering B. The vertical bar “|” means “given.”
P(B|A) (Likelihood): This is the probability of observing evidence B given that hypothesis A is true. It tells us how likely it is to see the evidence if our hypothesis is correct.
P(A) (Prior Probability): This is our initial belief about the probability of hypothesis A being true before we considered any evidence. It’s our prior knowledge or assumption about A.
P(B) (Evidence Probability or Marginal Likelihood): This is the probability of observing evidence B, regardless of whether hypothesis A is true or not. It acts as a normalizing constant. It can be a bit tricky to calculate directly sometimes, but it can be derived using the law of total probability (as shown in the code). It ensures that the posterior probability
P(A|B)is a valid probability (i.e., between 0 and 1).
In simpler terms:
Bayes’ Theorem tells us how to update our belief about a hypothesis (A) when we get new evidence (B).
It says that the updated belief (posterior probability P(A|B)) is proportional to our initial belief (prior probability P(A)) multiplied by how well the evidence supports the hypothesis (likelihood P(B|A)), and then normalized by the overall probability of seeing the evidence (P(B)).
Example:
Let’s say we’re trying to diagnose a medical condition.
A: The patient has the condition.
B: The patient tests positive for a certain marker.
P(A): The prior probability of someone having the condition (this might be based on population statistics).P(B|A): The probability of testing positive if the patient has the condition (this is the test’s sensitivity).P(B): The probability of testing positive (this could be due to having the condition or a false positive).P(A|B): The probability of the patient having the condition given they tested positive (this is what we really want to know).
Bayes’ Theorem helps us calculate P(A|B), the probability of having the condition after a positive test result, which is crucial for diagnosis.
Why is it important?
Bayes’ Theorem is essential because it provides a formal way to reason about probabilities and update our beliefs in the face of new information.
It’s a cornerstone of many statistical and machine learning techniques, and it’s a valuable tool for decision-making under uncertainty.